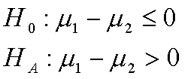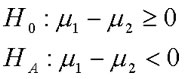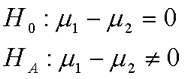t-test for Dependent Means

Hypothesis

The t-test for dependent means is used when we want to know whether there is a difference between populations when the data are "linked" or "dependent". For instance, we may want to know if using tutorials in a statistics class improves knowledge. To assess this, we would have to know a student's knowledge before using the tutorial and again after completing the tutorial. Thus, any data collect from this student are "linked". The t-test for dependent means is used only for tests of the sample means. Thus, our hypothesis tests whether the average difference between scores (M1 - M2) suggests that our students come from a population where tutorials do not affect performance (m1 - m2 = 0) or whether they come from a different population in which knowledge improves after using the tutorial.

The statistical hypotheses for t-tests for dependent means take one of the following forms, depending on whether your research hypothesis is directional or nondirectional. In the equations below m1 refers to the pre-test or Time 1 population from which the study sample was drawn; m2 refers to the post-test or Time 2 population.

Study Design

The t-test for dependent requires a specific type of research design. We use the t-test for dependent means when we collect data two different times on a single sample drawn from a population or when two different people are sampled as a pair because they are linked in some fashion in the population. In this design, we have one group of subjects/paired subjects, collect data on these subjects twice, compute the difference between pairs or pre-test and post-test scores, and compare the average sample difference (MDiff) to the population parameter (mDiff). The population parameter tells us what to expect if there was no effect or difference in the population. If our sample statistic is very different (beyond what we would expect from sampling error), then our statistical test allows us to conclude that our sample came from a population in which members of a pair were different or Time 1 and Time 2 scores were different. In the t-test for dependent means, we are comparing the mean difference (M1 - M2) calculated on linked/dependent data to an expectation that there is no difference in the population (m1 - m2 = 0).

Available Information

The t-test for dependent means compares the mean difference between sample scores that are linked by the study design to an expectation about the difference in the population. For this test, we do not need to know the population parameters. As long as the null hypothesis reflects no difference in the population, then the value of m1 - m2 needed for our statistical hypothesis is known (0). In t-tests, we estimate the population variances/standard deviations from sample data (S).

Test Assumptions

All parametric statistics have a set of assumptions that must be met in order to properly use the statistics to test hypotheses. The assumptions of the t-test for dependent means are listed below.

 Random sampling from a defined population
Interval or ratio scale of measurement
Population difference scores (m1 - m2) are normally distributed

 

When reading the psychological literature, we can find many studies in which all of these assumptions are violated. Random sampling is required for all statistical inference because it is based on probability. Random samples are difficult to find, however, and psychologists and researchers in other fields will use inferential statistics but discuss the sampling limitations in the article. We learned in our scale of measurement tutorial that psychologists will apply parametric statistics like the t-test on approximately interval scales even though the tests require interval or ratio data. This is an accepted practice in psychology and one that we use when we analyze our class data. Finally, the assumption that the difference scores are normally distributed in the population is considered "robust". This means that the the statistic has been shown to yield useful results even when the assumption is violated. The central limit theorem tells us that even if the population distribution is unknown, we know that the sampling distribution of the mean will be approximately normally distributed if the sample size is large. This also applies to the means of difference scores and helps to contribute to the t-test being robust for violations of normal distribution.

 

Click here to review the one-sample Z-test:
Click here to review the one-sample t-test:
Click here to review the t-test for independent means:
Click here to return to the main page: