This expression states that the variance is the mean of the squared deviations of the Xs (the measurements) from their mean. Hence the variance is sometimes referred to as the mean...squared deviation (of the measurements from their mean) or the mean square. The purpose of the derivation on this page is to obtain a computational forumla by expressing the variance in terms of descriptive moments only. We begin by squaring the binomial in the numerator of (1),
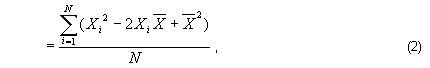
and then distributing the summation operator,
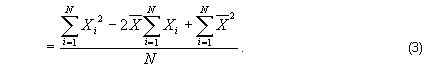
Notice that in the second term of the numerator, the 2 and the arithmetic mean have been factored out of the summation. This is because they are constants. Similarly, the last term in the numerator can be evaluated immediately because the arithmetic mean is a constant:
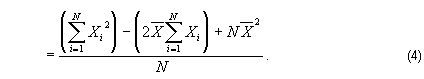
This is just an application of one of the rules of summation, viz., the sum of N like terms, a, is equal to N times a. Parentheses have been added to ensure that the summations are read correctly. Now, consider the definition of the arithmetic mean,
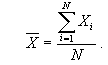
Solving this expression for the sum of the Xs gives
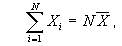
which can be substituted into the second term in the numerator of (4):
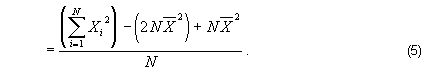
Combining the second and third terms in the numerator,
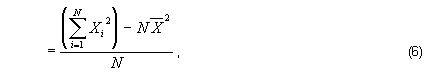
and substituting the definition of the arithmetic mean, given above, into the second term produces
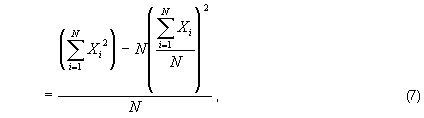
which simplifies to
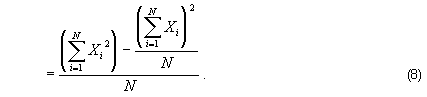
Hence, the computational formula for the variance is
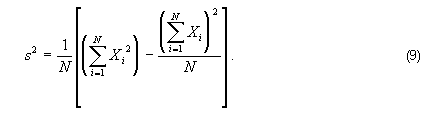
Here the variance is expressed in terms of the zeroth (N), first (sum of the Xs), and second (sum of the X-squareds) descriptive moments of the distribution only. No other terms or factors appear in the equation.
Back to Annotated Lecture Material and Supplementary Material.